2012 S2-05 Maths Blog
Monday, 8 October 2012
Tuesday, 2 October 2012
Friday, 28 September 2012
Tuesday, 25 September 2012
EOY
Here are some information about the paper:
Duration: 2 hr 30 min
Total marks: 100
40% of paper on Term 1 and 2 topics:
60% of paper on Term 3 and 4 topics:
Duration: 2 hr 30 min
Total marks: 100
40% of paper on Term 1 and 2 topics:
- Algebra and algebraic fractions
- Linear graphs
- Quadratic equations and graphs
- Area, perimeter, volume and surface area
- Pythagoras' Theorem
- Indices
60% of paper on Term 3 and 4 topics:
- Standard form
- Congruence and Similarity
- Area and volume of similar figures and solids
- Basic trigonometry
- Matrices
- Probability
- Simultaneous equations and graphs
- Set notation and venn diagrams
- Direct and inverse proportion
Set Language : Class CN-ECT activity
S205 Responses
Questions:
Do you agree with your friends' responses?
Some said F = J while others disagree? Comment.
Wednesday, 19 September 2012
Tuesday, 18 September 2012
Wednesday, 5 September 2012
Construction
Definition

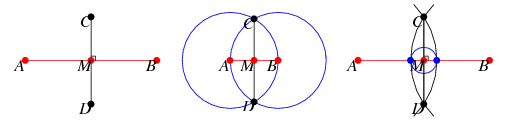
A perpendicular bisector

A. Constructing Perpendicular Bisector
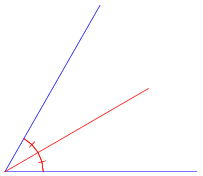
B Angles Bisector
Perpendicular Bisector

A perpendicular bisector  of a line segment
of a line segment  is a line segment perpendicular to
is a line segment perpendicular to 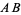 and passing through the midpoint
and passing through the midpoint 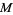 of
of 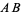 (left figure). The perpendicular bisector of a line segment can be constructed using a compass by drawing circles centered at
(left figure). The perpendicular bisector of a line segment can be constructed using a compass by drawing circles centered at 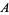 and
and 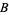 with radius
with radius 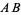 and connecting their two intersections. This line segment crosses
and connecting their two intersections. This line segment crosses 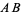 at the midpoint
at the midpoint 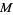 of
of 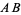 (middle figure). If the midpoint
(middle figure). If the midpoint 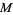 is known, then the perpendicular bisector can be constructed by drawing a small auxiliary circle around
is known, then the perpendicular bisector can be constructed by drawing a small auxiliary circle around 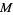 , then drawing an arc from each endpoint that crosses the line
, then drawing an arc from each endpoint that crosses the line 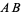 at the farthest intersection of the circle with the line (i.e., arcs with radii
at the farthest intersection of the circle with the line (i.e., arcs with radii 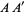 and
and 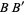 respectively). Connecting the intersections of the arcs then gives the perpendicular bisector
respectively). Connecting the intersections of the arcs then gives the perpendicular bisector 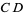 (right figure). Note that if the classical construction requirement that compasses be collapsible is dropped, then the auxiliary circle can be omitted and the rigid compass can be used to immediately draw the two arcs using any radius larger that half the length of
(right figure). Note that if the classical construction requirement that compasses be collapsible is dropped, then the auxiliary circle can be omitted and the rigid compass can be used to immediately draw the two arcs using any radius larger that half the length of 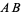 .Angle Bisector
.Angle Bisector

The (interior) bisector of an angle, also called the internal angle bisector (Kimberling 1998, pp. 11-12), is the line or line segment that divides the angle into two equal parts.
A. Constructing Perpendicular Bisector
B Angles Bisector
Monday, 27 August 2012
Direct and Inverse Proportion
Task 1
Part 1:
Explore the following graphs or information given and observe the following:
.1 patterns or repeated behaviours
.2 the variables exist in the information eg. time is changing
.3 the relationship between the variables
.4 is there a factor for change eg. values are tripled
Comment as a post
Comment as a post
information 1
information 2
information 3
information 4
information 5
Task 2: watch the following videos
Pa
Thursday, 16 August 2012
Subscribe to:
Posts (Atom)





.jpg)























